论文分享：Constraint-Driven-Auto-Tuning-of-GEMM-like-Operators-for-MT-3000-Many-core-Processor

1 概况

1.1 工作内容

针对新一代天河超级计算机所使用的核心芯片——MT-3000 众核处理器，进行“类 GEMM”算子优化的工作。

文中提出了一种 DynaChain 的深度学习（DL）算子编译优化框架，专门针对 MT-3000 这样的异构众核架构。

核心设计原则：计算与访存分离

1. 计算与访存解耦 (Decoupling Computation and Data Movement)

原理： 它将算子的“计算逻辑”与“数据搬运逻辑”分开处理。
作用： 这样可以独立优化这两者，从而在整个算子调度过程中最大限度地实现数据的全局复用，减少昂贵的内存访问开销。

2. 约束依赖链 (Constraint Dependency Chains)

原理： 在算子调度的搜索空间中，存在大量无效或次优的选项。DynaChain 通过引入“约束依赖链”来动态排除这些无效路径。
作用： 大幅缩小了优化算法的搜索空间，提高了寻找最优调度方案的效率。

3. 基于 ILP 的分解机制 (ILP-based Decomposition)

原理： 针对深度学习中常见的不规则矩阵维度（即矩阵的长宽不是 2 的幂次方或硬件向量长度的整数倍），使用整数线性规划进行任务分解。
作用： 避免了传统的“补零填充”（Padding）做法。补零会浪费计算资源，而这种分解方法能显著提升硬件的实际利用率。

4. 硬件感知微内核设计 (Hardware-aware Micro-kernel Design)

原理： 针对 MT-3000 的 VLIW（超长指令字）+ SIMD（单指令多数据流） 架构进行底层代码生成。
优化手段： 通过改进寄存器分配和指令流水线来支持复杂的算子操作。
作用： 确保生成的低级代码能够榨干硬件的原始性能。

AutoTVM，Ansor：在庞大的搜索空间中选择有效的“变换”（如循环展开、分块优化等），并结合运行时分析（Profiling）或成本模型（Cost Models）来自动寻找最优代码。

以上内容在主流的CPU和GPU有效。

DynaChain：轻量级算子级优化编译器

外部调度代码用 C 语言编写，使用多级 for 循环和 DMA 传输语句来管理任务调度、矩阵阻塞和数据移动。以汇编语言编写的内部微内核直接在硬件上执行计算密集型任务，并通过预定义的函数调用与外部调度代码连接。

1.2 两个挑战

1.数据移动策略、预取、批处理、流水线和重用需要协调 MT3000 多层内存层次结构 (DDR≻GSM≻AM≻SM) 中 111 多个参数的组合（参见表 1）。使用启发式算法（例如遗传算法）来使用 AutoTVM和 Ansor等自动调优器来探索这个 O (10^14) 调度搜索空间，但一种简单的基于搜索的方法无法对特定于硬件的依赖关系进行建模。AutoTVM 给出的探索计划中有 89% 违反了 GSM 容量 (M1 × K1 ≤ 6MB) 或 VLIW 寄存器限制 (μm × μn ≤ 64) 等约束。这会导致调优时间延长（GEMM >24 小时）和次优配置。

2.边缘情况下的矩阵大小不匹配问题。具体来说，当矩阵大小与微内核形状不匹配时，边缘情况通常需要额外的处理。例如4×144这种矩阵

1.3 解决方案

外层调度： 利用 自动调优来寻找数据搬运和任务划分的最佳方案。

内层计算： 结合专门针对硬件优化的微内核（Micro-kernel），确保底层的每一条指令都发挥最大效能。

核心技术 A：约束依赖链

1.捕捉参数之间的相互依赖关系（例如：如果分块大小 A 选了某个值，那么分块大小 B 必须在某个范围内）。

2.构建一个经过拓扑排序的依赖图。

3.通过这个图，算法可以提前发现哪些组合是“死路”并直接剪枝，从而极大地缩小了搜索范围，显著加快了找到最优配置的速度。

核心技术 B：基于 ILP 的计算分解

将一个大任务分解成多个不同形状的微内核组合。比如一个不规则的矩阵，可以用“一个大方块 + 几个长条 + 几个小点”来完美覆盖。

核心技术 C：改进 mtBLAS 微内核

1.4 结论

DynaChain 生成的代码可实现高达硬件理论峰值性能的 93%，提供与特定于供应商的手动调整库相当的性能，但人工参与较少。

核心贡献：

1.针对复杂架构的新型编译优化策略

核心动作： 提出了一种基于编译器的算子优化策略。
适用对象： 拥有多级存储和 SIMD+VLIW 架构的硬件（即 MT-3000）。
技术手段： 通过计算与数据搬运的解耦，实现了数据的全局复用。
最终结果： 让深度神经网络算子的执行效率接近硬件的峰值性能。

2. 引入约束依赖链

解决痛点： 优化参数太多，搜索空间太大（就像在无边无际的荒野里找金矿）。
创新点： 提出 CDC 技术，利用动态推导出的约束条件之间的相互依赖关系。
效果： 极大地缩小了搜索空间，让自动调优变得飞快。

3. 基于 ILP 解决形状不匹配问题

解决痛点： 矩阵的大小（Shape）往往和底层硬件最擅长处理的计算块（Micro-kernel）大小对不上（比如硬件喜欢 8x8，但数据是 7x9）。
创新点： 将“如何用不同的微内核拼凑出目标矩阵”变成一个整数线性规划数学问题。
效果： 显著提升了不规则矩阵或小规模矩阵在硬件上的运行效率，避免了浪费。

4. 改进针对 MT-3000 的底层微内核设计

核心动作： 对最底层的微内核（Micro-kernel）进行了重构。
硬件适配： 专门针对 MT-3000 的特性，优化了计算和访存的效率。
突破： 即使是在处理不规则形状的数据时，也能保持极高的指令并行度和吞吐量。

2 背景及相关情况介绍

2.1 MT-3000硬件架构

GP 区 (General-Purpose Zone)：

包含 16 个通用 CPU 核心。

ACC 区 (Acceleration Zone)：

共有 4 个加速区（集群）。
每个加速区包含 24 个加速阵列 (Acceleration Arrays)。
存储资源： 每个加速区拥有 6MB 片上全局共享内存 (GSM)、48MB 高带宽共享内存 (HBSM) 和 32GB 片外 DDR 内存。
访问限制： 这是一个关键点——虽然 CPU 可以访问所有内存，但加速阵列只能访问自己所属集群内的资源。

A. 标量处理单元 (SPU)

负责：指令流控制和基础的标量运算。
存储：拥有独立的 64KB 标量存储器 (SM)。

B. 向量处理单元 (VPU)

SIMD 模式： 拥有 16 个向量处理元件 (VPE)。
计算能力： 每个元件有 64 个向量寄存器和 3 个向量浮点乘加单元 (VFMA)。这是处理深度学习中大量矩阵运算的“主力军”。
存储： VPU 只能访问 阵列存储器 (AM)。

C. DMA 引擎

负责在不同的存储层级（如 DDR、GSM、AM）之间搬运数据。

访存隔离

SPU 只能访问 SM。
VPU 只能访问 AM。

2.2 矩阵优化

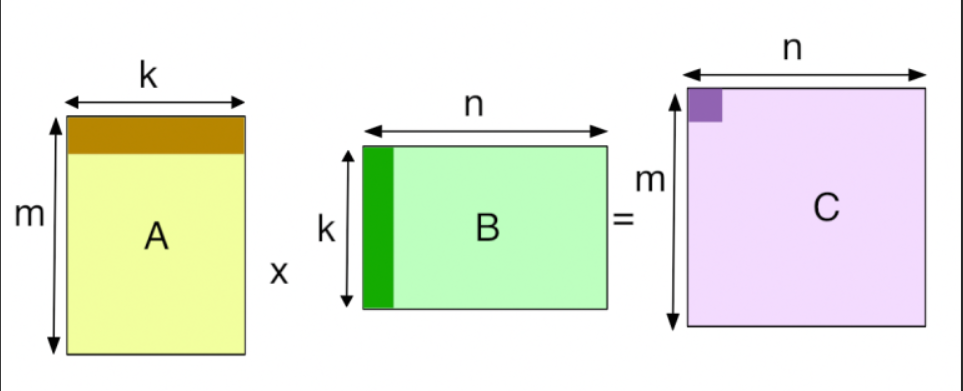
GEMM运算表示为C+=A·B，其中A和B是输入矩阵，C是被输出覆盖的矩阵。在这项工作中，遵循线性代数库中使用的命名约定，其中矩阵 A 是具有 M 行和 K 列的 M × K 矩阵，矩阵 B 是 K × N ，矩阵 C 是 M × N 。

外部调度代码如下：

首先，A 的子矩阵存储在 GSM 中，由于跨内核共享，因此可以实现数据重用，从而减少冗余内存负载并加快数据访问速度。此外，矩阵A和B的计算也采用了流水线，分为加载和计算两个阶段。类似地，矩阵C的计算分为三个流水线阶段：加载、计算和存储。每个阶段都有一个专用的缓冲区，以确保高效的数据访问。通过将数据预取和流水线结合起来，可以重叠加载、计算和存储操作，从而减少等待时间并提高计算效率。关于内存布局，矩阵A存储在SM中，以支持高效的基于列的访问，按照微内核中使用的外积方法的要求。矩阵 B 存储在 AM 中以利用基于行的访问，这与 AM 有效处理基于向量的运算的能力相一致。

内核实现示意图：

微内核使用外积方法实现，每次迭代时选择矩阵 As 中的一列和矩阵 Ba 中的一行进行计算。结果通过 μk 次迭代进行累积，然后将最终计算值写入 AM 中。

2.3 研究动机

结合微内核可以避免填充浪费并提高硬件利用率。 GEMM 中的边缘情况经常会降低硬件利用率。如下图

1.DynaChain 通过动态微内核组合解决了这些限制（将 4×144 矩阵填充到 4×192 以与 3×64 内核兼容，从而将利用率降低至 50%。虽然辅助微内核（图 5(b)）以残差块（例如 1×64 或 4×16）为目标，但由于管道使用效率低和优化差距，它们通常表现不佳，利用率仅为 67%。），它在运行时结合优化的内核形状（例如 4×64+4×80）以精确匹配不规则矩阵尺寸。

2.DynaChain 通过将计算与数据移动解耦来解决这个问题。这种分离允许全局共享缓冲区和跨块的重用感知调度，减少冗余负载并提高整体吞吐量。

3.探索各种调度参数（例如，块大小、展开因子）的组合，但由于调度参数的指数增长而产生过高的开销。每个节点强制执行模块化约束（例如 MOD(M3, μm)）并消除违反该约束的值（删除）。有效的参数选择向下传播，而 AND 运算确保必须共同满足所有跨维度约束。例如，在 GEMM 分块中，如果 M3 不能被微内核大小 μm 整除，则所有依赖于 M3 的上层块大小（M2，M1）将立即被剪枝。

2.4 DynaChain工作流程

第一阶段：算子映射模块 (Operator Mapper)

这个模块负责把“数学公式”变成“初步的计算逻辑”。

①基础映射： 将输入的算子转化为简单的、嵌套的多层循环实现。这是最原始的代码形态。
②计算分解（重点）： 利用之前提到的 ILP（整数线性规划） 方法，把大矩阵拆解成一个个子块。每个子块都对应一个特定形状的微内核调用。

第二阶段：自动调优模块

这是 DynaChain 能够从 111+ 个参数中找到最优解的关键。

③参数化策略： 识别所有与数据搬运相关的优化手段，并把它们变成可调的参数，从而构建出一个巨大的搜索空间。
④拓扑排序： 确定这些优化策略的执行顺序。通过拓扑排序，确保参数之间有先后逻辑，形成约束依赖链的雏形。
⑤构建依赖树： 自动推导出参数之间的约束关系，形成一个树状的链式结构。
⑥高效搜索（剪枝）： 在搜索最优参数时，利用这个依赖链进行“导航”。一旦发现某条路径违反了约束（比如内存放不下了），就立即停止（Pruning/剪枝）并回溯。这让搜索速度大幅提升。

第三阶段：微内核生成模块 (Micro-Kernel Generator)

这个模块负责编写最底层的、直接操作硬件寄存器的指令。

⑦高性能生成： 针对 MT-3000 的 VLIW+SIMD 架构，设计并生成能够处理不规则形状的高性能微内核。这些内核经过极致优化，负责完成最后的数值计算。

3 外部实现原理

3.1 算子映射

目标是将DNN等类GEMM的算子映射为GEMM形式

A. 数据重塑 (Data Reshape)

动作： 调整数据的访问顺序（逻辑布局）。
要点： 虽然它改变了代码“看”数据的方式，但并没有改变数据在内存中的实际存储物理顺序。
目的： 优化访问性能，让数据读取更符合硬件的缓存或寄存器特性。

B. 索引映射 (Index Mapping)

动作： 通过数学公式，将原始的多维坐标（如图片的通道、高、宽）映射到目标形状的线性索引上。
目的： 将复杂的几何运算摊平成一维或二维的数学运算。

以卷积算子为例

卷积涉及非常多的维度：

原始索引 (I, F, O)： 通常指输入张量、卷积核、输出张量。
循环变量 (x, c, h, w, l, r, s)： 代表 Batch 大小、通道、高度、宽度、卷积核半径等。

通过特定的映射关系，这些变量被压缩成了 $m, n, k$ 三个变量：

映射到 $m$ (输出空间维度)：

将图片的空间位置（ $h, w$ ）和 Batch 索引（ $x$ ）合并。

公式： $m = x \cdot H \cdot W + h \cdot W + w$

这相当于把一张三维的图片“拉直”成矩阵的一行或一列。
映射到 $k$ (缩减维度/内积维度)：

将通道索引（ $c$ ）和卷积核内部的偏移（ $r, s$ ）合并。

这对应于卷积核在特定窗口内进行点积的那些元素。
映射到 $n$ (输出通道维度)：

将输出通道（ $l$ ）映射到 $n$ 。

最终可以得到

for (int m = 0; m < M; ++m) {
    for (int n = 0; n < N; ++n) {
        for (int k = 0; k < K; ++k) {
            // 核心计算：C[m][n] += A[m][k] * B[k][n]
        }
    }
}

编译器只需要重点优化“三层循环矩阵乘法”这一种模式，就能同时解决所有算子的性能问题。

3.2 计算分解

文中提出了一种基于整数线性规划的简单而有效的计算分解方法，确保即使不规则的矩阵形状也能得到有效处理。给定输入数据 D (M × N )，分解的目标是将其划分为几个大小为$μ^i_ m × μ^i_n $的块（其中 i 表示第 i 个微内核候选者），确定块的数量 ($ num_i$ )，并相应地排列它们。

步骤 1：对候选微内核进行排名。由于向量寄存器的限制，微内核不能任意大，并且可能的微内核形状的数量是有限的。因此提出了一个轻量级性能模型（参见等式（1））来对这些候选者进行排名。

VL 表示 SIMD 数据通道——向量寄存器可以保存的单精度和双精度浮点数的数量。 u是循环展开因子，表示微内核中循环展开了多少次。 $μ^i_k$ 是微内核候选中的循环迭代次数，而 $μ^i_{ku}$ 是微内核候选中展开后的循环迭代次数。 #MACs 表示 VFMA 单元的数量。更高的性能分数对应于选择微内核候选者的更高优先级。排名是基于这些优先级的。

步骤 2 ：

为了将一个大小为 $M \times N$ 的大矩阵拆解成多个小的微内核块，DynaChain 定义了以下变量：

候选尺寸 ( $\mu_m^i, \mu_n^j$ )：代表硬件支持的各种微内核的高度和宽度候选值。

决策变量 ( $z_{ij}$ )：代表形状为 $(\mu_m^i, \mu_n^j)$ 的微内核块被使用了多少次。

\max \sum_{i=1}^{s_m} \sum_{j=1}^{s_n} \text{score}(\mu_m^i, \mu_n^j) \cdot z_{ij}

每个形状的微内核都有一个“评分”（Score），代表它在硬件上的执行效率。目标是找到一种组合，使得总评分最高，即整体执行效率最高。

为了实现“精确覆盖”（Exact covering）并避免对齐错误或补零，要求选出的所有微内核块在宽度方向的总和必须等于 $N$ ，在高度方向的总和必须等于 $M$ 。

步骤 3 :

如果直接解上述方程组，可能会忽略微内核的“形状优先级”。DynaChain 引入了一种优先级层次方法：

先解决 $N$ 维度（宽度）：首先确定合适的宽度 $\mu_n^j$ 来满足宽度的约束。
再解决 $M$ 维度（高度）：在确定了宽度之后，再选择相应的高度 $\mu_m^i$ 。
动态调整：这种方法可以动态地调整微内核的布局，确保即使是形状非常奇特的小矩阵，也能被高效地划分并对齐。

ILP 求解器的性能表现：

测试规模：针对 1000 个随机采样的算子形状（从 $32 \times 32$ 到 $512 \times 512$ ）进行了测试。
求解速度：中位求解时间仅为 0.42 秒，说明该算法非常轻量，不会显著增加编译负担。
优化质量：97.8% 的案例达到了理论上的最优解；其余案例与最优解的性能差距也小于 0.4%。

3.3 参数优化策略

3.3.1 多级内存的循环优化

Loop Split (循环拆分)： 将大循环拆小以增强数据局部性。关键参数是不同内存层级的 Split Size。

Loop Reorder (循环重排)： 改变循环嵌套顺序（如将 $m, n, k$ 变为 $n, k, m$ ）来优化缓存访问。

Loop Unroll (循环展开)： 展开循环体以增加指令级并行，关键参数是 Unrolling Factor。

3.3.2 数据流优化

Data Prefetching (数据预取)： 在需要数据前提前加载，减少内存延迟。关键参数是 Prefetch Distance。

Pipelining (流水线)： 将任务分为多个阶段并行执行，实现计算与通信的重叠（Overlapping）。

DMA Communication (DMA 通信)： 直接控制不同存储层级间的数据搬运。涉及参数包括传输的起始/目标地址、行数、列数、步长（Stride）以及使用的通道数。

3.3.3 内存优化

Data Layout (数据布局)： 优化数据在内存中的存储方式，关键参数是 Access Pattern（访问模式）。

SPM Management (SPM 管理)： 针对 MT-3000 特有的暂存存储器（Scratchpad Memory）进行管理。通过控制 Buffer 的数量、行数和列数，确保高效的数据移动。

3.4 构建约束依赖链

由于架构限制（如内存容量、DMA对齐、核形状可整除性），并非所有参数组合都有效。为了提前修剪不可行配置，DynaChain构建了约束依赖链（CDC）——一种有向无环图（DAG）

由于优化策略对参数施加的限制，识别约束依赖关系可以简化，以确定策略间的依赖关系。每种策略都可能影响其他策略的执行顺序或参数设置，形成依赖关系。这些依赖关系可以分为顺序依赖或双向依赖。

顺序依赖意味着某些策略（例如数据布局）必须先执行以确保数据正确排列
双向依赖则表示一种策略的执行可能影响另一种策略的参数或状态。

数据布局→SPM管理;

流水线→数据预取;流水线→SPM管理;《循环展开→流水线化》;

循环拆分→循环重排→循环展开;

为了枚举所有可能的序列，文章使用Kahn’s algorithm进行拓扑排序

3.4.1 卡恩算法：

统计入度：遍历图中所有边，计算每个节点的入度。

初始化队列：将所有入度为 0 的节点放入一个队列（Queue）中。

循环处理：

从队列中取出一个节点（记为 $u$ ），将其放入结果序列中。
遍历节点 $u$ 的所有邻居节点（记为 $v$ ）。
由于 $u$ 已经被处理，模拟“删除” $u$ 到 $v$ 的边，即将 $v$ 的入度减 1。
如果减 1 后， $v$ 的入度变为 0，则将 $v$ 放入队列。

检查循环：

如果最终结果序列中的节点数等于图中的总节点数，说明排序成功。
如果节点数少于总节点数，说明图中存在环（Cycle），导致某些节点入度永远无法归零。

3.4.2 约束生成机制

1.约束的分类：已知 vs 未知

DynaChain 根据约束的确定时间将其分为两类：

已知约束 (Known Constraints)：
- 定义：在优化开始之前就已经确定的物理或逻辑限制。
- 例子：由算子映射器确定的微内核大小。
- 处理方式：在调度过程中必须严格遵守。
未知约束：
- 定义：在在线优化过程中动态发现或定义的更复杂的限制。
- 处理方式：根据预设的“自定义生成规则”动态产生。

2.具体的约束规则示例

文中提到了三个典型的硬件相关约束，这些约束直接影响计算性能：

Mapping-1（对齐约束）：确保计算中的分块大小（ $m_i, n_i, k_i$ ）必须是微内核形状（ $\mu_m, \mu_n, \mu_k$ ）的整数倍。这能避免处理边界碎片，从而达到近乎完美的计算效率。
Mapping-2（传输对齐）：确保矩阵缓冲区（Buffer）的行和列与 DMA（直接内存存取） 传输的行列对齐。这能保证数据在内存和处理器之间搬运时效率最高。
MemCapacity（内存容量）：硬性指标，确保每个层级的缓冲区大小都不会超过该级硬件内存的实际容量。

3.硬约束 vs 软约束

DynaChain 不仅关注“能不能跑通”，还关注“跑得快不快”：

硬约束 (Hard Constraints)：必须满足（如内存容量），不满足则方案不可行。
软约束 (Soft Constraints)：实际上是优化目标。
- MaxPerf：最大化微内核的运算密度，追求硬件极限。
- MinRemainMem：最小化剩余内存，即最大化内存利用率。

4.约束的表达工具（算术与逻辑运算）

为了将这些复杂的规则转化为计算机可理解的指令，DynaChain 使用了一系列操作符来缩减“调度空间”：

一旦构建完CDC，调优器会按照拓扑排序顺序探索参数组合。在每一步，参数会根据其约束进行评估。如果参数违反任何硬约束，当前路径会立即被修剪。如果一个约束依赖于之前无效的约束（例如，约束A→约束B），那么完全跳过约束B。软约束用于优先考虑空间中有潜力的区域。例如，如果配置未能达到MaxPerf定义的性能阈值，可以根据搜索策略提前降优先级或修剪。这种CDC指导的剪枝大幅缩小了搜索空间。

3.5 举例

3.5.1 图示解析：从混沌到有序

Candidate Space (候选空间)：左侧绿色的点代表所有可能的参数组合。如果不加约束，搜索空间非常巨大（本例中为 1296 种）。
CDC (约束依赖链)：中间的树状图展示了参数间的层次依赖。
- 根节点到 $\mu_m, \mu_k$ （微内核大小）。
- 向下延伸到不同层级的分块大小（ $M_3, M_2, M_1$ 等）。
Pruned Space (剪枝后的空间)：右侧展示了经过约束过滤后剩下的少数可行方案。

3.5.2 约束规则：必须遵守的“军规”

例子中定义了两类核心约束：

层级整除约束 (Layer-wise Divisibility)：
- 上层分块必须能被下层整除。例如 $\mu_m | M_3$ （ $M_3$ 必须是 $\mu_m$ 的倍数）， $M_3 | M_2$ ，以此类推。
- 这保证了数据分块能够完美对齐，没有多余的边角料。
容量约束 (Capacity Constraint)：
- 硬件内存是有限的。例子中要求 $M_2 \cdot K_2 \le 5000$ 。如果组合超过这个值，程序会崩溃（Out of Memory）。

3.5.3 剪枝过程演示

文中举了一个非常直观的例子：

如果不剪枝（暴力枚举）：

所有参数的可能性相乘： $2 \times 2 \times 3 \times 2 \times 3 \times 3 \times 2 \times 3 = \mathbf{1296}$ 种组合。
使用 CDC 剪枝：

假设我们选了 $M_3 = 24$ 。
1. 整除检查： $M_2$ 的候选值有 $\{64, 96\}$ 。因为 $64 \div 24$ 除不尽，所以 $M_2$ 被迫只能选 96。
2. 容量检查：此时看 $K_2$ $K_{2}$ （可选 $\{64, 96\}$ ${64, 96}$ ）。
  - 如果选 64： $96 \times 64 = 6144 > 5000$ （失败）。
  - 如果选 96： $96 \times 96 = 9216 > 5000$ （失败）。
3. 结果：一旦 $M_3 = 24$ 这个节点失败了，它下面连接的所有 $M_2, M_1$ 的组合都不用再看了。

3.5.4 结论

空间压缩：原本 1296 种组合，经过 CDC 过滤后只剩下 144 种。
剪枝率：成功减掉了 88.9% 的无效搜索空间。
性能意义：这意味着调优工具不需要在硬件上运行那 1152 种错误的配置，极大地缩短了寻找最优算子配置的时间。

4 微内核设计

核心约束（C1 - C4）的改进

作者对比了 mtBLAS 的原始约束，并提出了四个关键修改点：

C1：寄存器压力优化
- 改进：现在只需要 $4u$ 个向量寄存器（ $u$ 是循环展开因子），其中 $2u$ 用于加载矩阵 $A$ 的数据， $2u$ 用于加载矩阵 $B$ 。
- 原理：利用加载指令（Load）的最后一个周期直接将结果存入寄存器，减少了寄存器的总占用量。
C2 & C3：计算单元（VFMA）利用率
- 改进：原本只考虑 $\mu_m$ 和 $\mu_n$ （分块的高和宽），现在引入了 $\mu_k$ （深度）。
- 目的：确保配置是 VFMA（向量融合乘加）单元数量的倍数，从而充分利用 MT-3000 的三个 VFMA 单元。
C4：指令流水线填充
- 改进：采用循环展开技术。
- 目的：确保主循环中充满指令，避免处理器流水线出现空转。

参数化微内核生成器

为了实现自动化优化，作者开发了一个生成器，它会在 MT-3000 的硬件限制内尝试各种组合：

搜索空间：
- $\mu_m$ （行方向分块）： $1$ 到 $20$ 之间。
- $\mu_n$ （列方向分块）： $1$ 到 $768$ 之间。
硬性预算限制（寄存器限制）：
- 累加器限制： $\frac{\mu_m \cdot \mu_n}{VL} \le 64$ （其中 $VL$ 是向量长度）。
- 完整压力模型： $4u + \frac{\mu_m \cdot \mu_n}{VL} \le 64$ 。这确保了展开因子和计算所需的寄存器总数不会超过硬件物理上限。
深度优化： $\mu_k$ 不设固定限制，交给调优器（Tuner）去寻找吞吐量最优的深度。

性能与效率平衡

缓存机制：虽然支持任意形状，但作者发现有几种形状在实际工作中占统治地位。
策略：将最常用的 8 种形状缓存为静态内核，从而消除了运行时重新生成内核的开销。

所有内核均可实现超过 310 GFLOPS，其中表现最佳的形状达到硬件峰值的 99.5%。

5 讨论和结论

5.1 DynaChain 的运行开销

计算分解：这个过程几乎是瞬时完成的，不占用额外时间。
调度空间探索：得益于前面提到的 CDC 剪枝技术，系统能快速排除那些表现不佳的候选方案。整个搜索过程可以控制在 2 分钟以内。
代码生成：这部分发生在编译阶段，消耗的时间微乎其微，可以忽略不计。

5.2 广泛适用性与架构关联

虽然该研究是基于 MT-3000 平台开发的，但其核心思想具有通用性：

核心理念通用：基于约束的调度（Constraint-based scheduling）和整数线性规划（ILP）建模的方法可以推广到其他硬件架构。
深层存储层级/向量化硬件：在具有复杂存储结构或显式向量化指令（如 VLIW 或 SIMD）的系统中，这种方法有助于挖掘并行性并减少数据搬运（Data Movement）。
计算与访存分离：对于采用“计算与访问路径解耦”设计的架构，DynaChain 将计算与通信分离的思想也能带来显著收益。

5.3 移植到新平台的考虑

如果你想把这个自动调优器移植到其他平台（比如 NVIDIA GPU 或其他国产芯片），需要做以下调整：

需要更改的部分：主要提供新硬件的特定参数。
- 硬件参数：包括缓存大小、有效内存带宽、指令延迟等。
- 代价模型：需要输入这些参数来评估不同方案的优劣。
保持不变的部分：求解器和调度逻辑无需修改，具有很强的复用性。
针对 GPU 的特别优化：
- 如果移植到 GPU，需要将约束条件从当前的“内存容量限制”转向 GPU 关注的特征：线程/线程块并行度、共享内存分块以及合并访问模式。