【CUDA】(三)CUDA执行模型
(三)CUDA执行模型
本篇笔记参考如下:
https://face2ai.com/program-blog/#GPU编程(CUDA)
本章内容概览:本章内容:
·通过配置文件驱动的方法优化内核
·理解线程束执行的本质
·增大GPU的并行性
·掌握网格和线程块的启发式配置
·学习多种CUDA的性能指标和事件
·了解动态并行与嵌套执行
3.1 CUDA执行模型概述
CUDA执行模型揭示了GPU并行架构的抽象视图,使我们能够据此分析线程的并发。
3.1.1 GPU架构概述
Fermi SM的关键组件:
·CUDA核心
·共享内存/一级缓存
·寄存器文件
·加载/存储单元
·特殊功能单元
·线程束调度器
示例图如下:
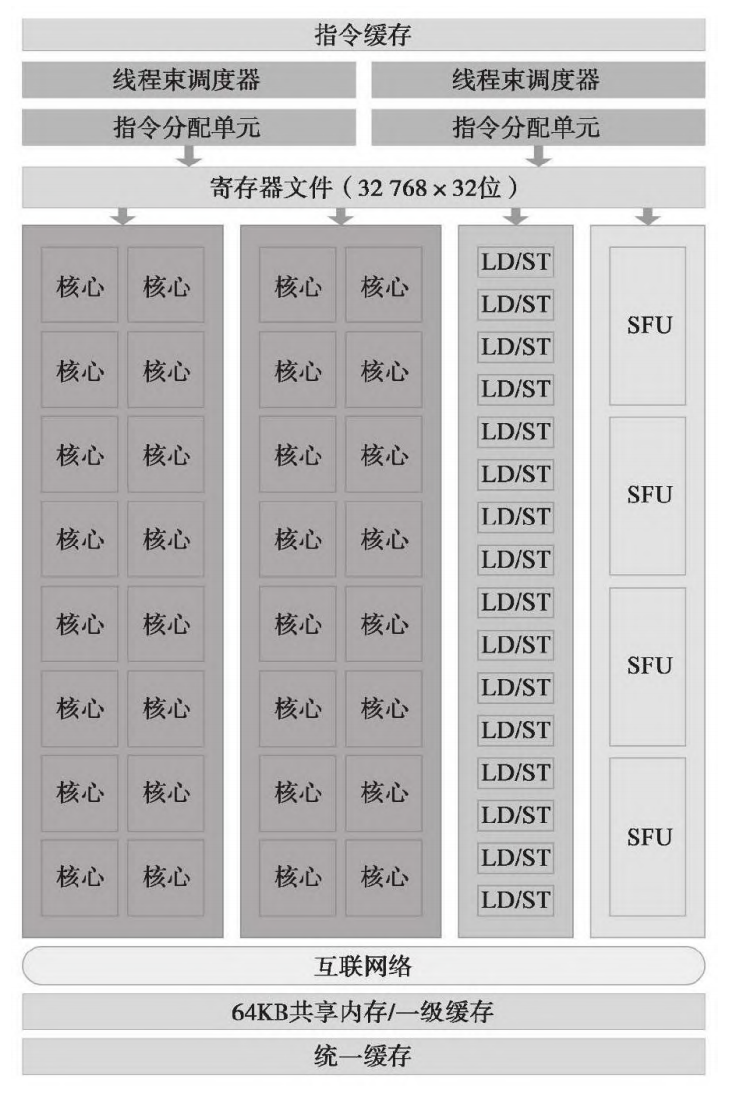
Blackwell的关键组件
- CUDA 核心:
- 第五代张量核心:
- 新增/关键组件:这是 Blackwell 的核心进化点。
- 寄存器文件 :
- 用于存储线程状态和操作数。
- Blackwell 维持了极大的寄存器规模,以支撑高并发的线程执行(尽管具体的 GB206 每个 SM 寄存器总量通常延续自上一代的 64K 或更高规格)。
- 共享内存/一级数据缓存:
- 采用统一的存储结构。
- Blackwell 进一步优化了共享内存的带宽和延迟,允许开发者通过显式编程实现 SM 内部线程间的高效数据交换。
- 特殊功能单元 (SFU - Special Function Units):
- 负责执行超越函数(如 , , , )以及图形插值指令。
- 加载/存储单元 (LD/ST Units):
- 负责在寄存器和存储层级(L1/L2/显存)之间搬运数据。
- 第四代光线追踪核心 (4th Gen RT Cores):
- 专用组件:负责硬件级加速射线/三角形相交测试和包围盒遍历。
- Blackwell 的 RT Core 引入了微掩码遍历(Micro-mask Traversal)以提升渲染效率。
- 线程束调度器与分发单元 (Warp Schedulers & Dispatch Units):
- 负责管理线程束(Warp)的执行序列,并将指令分发到对应的执行单元(CUDA 核心、Tensor 核心等)。
- Transformer 引擎 2.0 (Transformer Engine):
- 新增组件:这是 Blackwell SM 内部的一套智能管理逻辑。
- 它能自动监控算子执行过程中的数值分布,并在 FP4、FP8 和 FP16 等精度间动态切换,以在不损失精度的前提下实现最高计算强度。
了解硬件的具体参数有助于最大化开发硬件性能。
采用测试代码test.py得到本机参数
1 | import torch |
可以得到如下结果
| 参数类别 | 硬件参数名称 | 规格数值 | 备注 / 技术说明 |
|---|---|---|---|
| 核心配置 | 显卡型号 | RTX 5060 Ti | 基于 Blackwell 架构 (GB206 核心) |
| 计算能力 (CC) | 12.0 | 决定了可使用的指令集和硬件特性限制 | |
| SM 数量 | 36 | 流式多处理器的总数 | |
| CUDA 核心总数 | 4608 | 计算公式: | |
| 线程限制 | 每 SM 最大线程数 | 1536 | 硬件并发极限,由 48 个 Warp (32 线程/Warp) 组成 |
| 每 SM 最大 Block 数 | 32 | 即使线程没满,Block 数量也不能超过此值 | |
| 每 Block 线程上限 | 1024 | 软件定义 blockDim 时允许的最大值 |
|
| 存储资源 | 总显存容量 | 约 16 GB | 对应您检测到的 16311 MB |
| 每 SM 共享内存 | 128 KB | 用于线程块内通信,可配置 L1 缓存比例 | |
| 每 SM 寄存器总量 | 64K | 32-bit 寄存器,决定了 Kernel 的复杂度上限 |
注意:一个sm有128个cuda核心,一个sm最多可以承载48个wrap,一个wrap有32个线程
重要知识
注意 32 这个数字,是SM用SIMD方式所同时处理的工作粒度。优化工作负载以适应线程束(一组有32个线程)的边界,一般这样会更有效地利用GPU计算资源。
1.一个线程块只能在一个SM上被调度。一旦线程块在一个SM上被调度,就会保存在该SM上直到执行完成。
2.在同一时间,一个SM可以容纳多个线程块。
3.在SM中,共享内存和寄存器是非常重要的资源。共享内存被分配在SM上的常驻线程块中,寄存器在线程中被分配。
4.线程块中的线程通过这些资源可以进行相互的合作和通信。
5.线程块里的所有线程都可以逻辑地并行运行,但是并不是所有线程都可以同时在物理层面执行。
6.尽管线程块里的线程束可以任意顺序调度,但活跃的线程束的数量还是会由SM的资源所限制。SM可以从同一SM上的常驻线程块中调度其他可用的线程束。在并发的线程束间切换并没有开销,因为硬件资源已经被分配到了SM上的所有线程和块中,所以最新被调度的线程束的状态已经存储在SM上。
这里我有一些自己的疑问
**疑问1:**如果分配了2个有8个线程的线程块,他们会被分配给一个线程束吗?
得出的结果是:
Block 0 (8个线程): 会占用 1 个完整的工作线程束。其中只有前 8 个线程在干活,剩下的 24 个槽位处于“闲置”状态(但在硬件占用上,这 32 个位置都被占用了)。
Block 1 (8个线程):会占用 另一个完整的工作线程束。同样,只有 8 个线程活跃,24 个闲置。
疑问2:两个线程块,每个线程块40个线程,会怎么分配?
答案是:
| 归属对象 | 线程编号 | 消耗的 Warp 资源 | 活跃状态 |
|---|---|---|---|
| Block 0 | 0 ~ 31 | Warp 0.0 | 32 线程全开(满载) |
| Block 0 | 32 ~ 39 | Warp 0.1 | 8 线程活跃,24 线程空转 |
| Block 1 | 0 ~ 31 | Warp 1.0 | 32 线程全开(满载) |
| Block 1 | 32 ~ 39 | Warp 1.1 | 8 线程活跃,24 线程空转 |
3.2 线程束的本质
在内核中可以看作所有的线程都是并行地运行。在逻辑上这是正确的,但从硬件的角度来看,不是所有线程在物理上都可以同时并行地执行。
3.2.1 线程束和线程块
线程束是SM中基本的执行单元。当一个线程块的网格被启动后,网格中的线程块分布在SM中。
一个线程束由32个连续的线程组成,在一个线程束中,所有的线程按照单指令多线程(SIMT)方式执行;也就是说,所有线程都执行相同的指令,每个线程在私有数据上进行操作。如图所示:
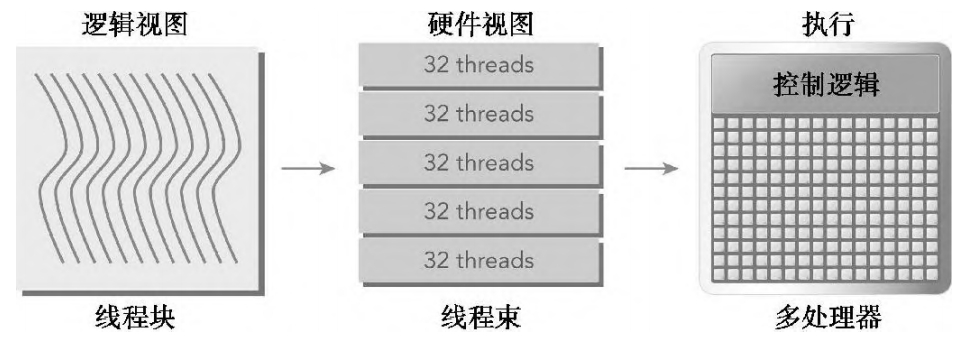
对于一个线程块来说,可以被配置为一维、二维或三维的。
想象下c语言的数组,如果把上面这句话写成c语言,假设三维数组t保存了所有的线程,那么(threadIdx.x,threadIdx.y,threadIdx.z)表示为
1 | t[z][y][x]; |
1.计算出三维对应的线性地址是:
2.如果是二维,可以看作为0,得到如下地址:
3.如果是一维,可以看作,为0,得到如下地址:
对于网格来说,同样可以配置为一维、二维或三维的。
1.三维情况下:
全局坐标计算:
线性索引公式:
2.二维情况下,z为0:
全局坐标计算:
线性索引公式:
3.一维情况下,y,z为0:
直接得到索引:
3.2.2 线程束分化
控制流是高级编程语言的基本构造中的一种。GPU支持传统的、C风格的、显式的控制流结构,例如,if…then…else、for和while。
CPU拥有复杂的硬件以执行分支预测,也就是在每个条件检查中预测应用程序的控制流会使用哪个分支。
GPU是相对简单的设备,它没有复杂的分支预测机制。一个线程束中的所有线程在同一周期中必须执行相同的指令,如果一个线程执行一条指令,那么线程束中的所有线程都必须执行该指令。

对以上代码来说,假设在一个线程束中有16个线程执行这段代码,cond为true,但对于其他16个来说cond为false。一半的线程束需要执行if语句块中的指令,而另一半需要执行else语句块中的指令。在同一线程束中的线程执行不同的指令,被称为线程束分化。
对于GPU来说,无法同时指挥两拨线程做不同的动作。于是硬件会采取 “轮流执行” 的策略:
- 第一步(执行 if 分支):
- 指挥官发出
if路径的指令。 - 硬件掩码(Masking):属于
else路径的 16 个线程会被强制禁用(挂起状态,不进行计算,也不写回结果)。 - 此时,只有 16 个线程在干活,但消耗的时间是 32 个线程的执行时间。
- 指挥官发出
- 第二步(执行 else 分支):
- 指挥官切换指令,发出
else路径的指令。 - 硬件掩码切换:轮到刚才做
if的 16 个线程被禁用,原来挂起的 16 个线程开始干活。 - 此时,另外 16 个线程在干活,同样消耗 32 个线程的执行时间。
- 指挥官切换指令,发出
最终结果:原本可以并行的代码,因为这个 if 变成了串行(Sequential)。总耗时 = if 耗时 + else 耗时。
注意,线程束分化只发生在同一个线程束中。在不同的线程束中,不同的条件值不会引起线程束分化。
举例
用一个偶数和奇数线程方法来模拟一个简单的数据分区,目的是导致线程束分化。
1.该条件(tid%2==0)使偶数编号的线程执行if子句,奇数编号的线程执行else子句。核函数为:
1 | __global__ void mathKernel1(float *c) |
2.使用线程束方法(而不是线程方法)来交叉存取数据,可以避免线程束分化,并且设备的利用率可达到100%。条件(tid/warpSize)%2==0使分支粒度是线程束大小的倍数。核函数为
1 | __global__ void mathKernel2(float *c) |
1 | 设备上第一次运行可能会增加间接开销,并且在此处测量的性能是非常精细的,所以,添加了一个额外的内核启动(warmingup,与mathKernel2一样)来去除这一间接开销。 |
负载如下:
1 | int size = 1 << 24; |
编译并运行simpleDivergence.cu
1 | nvcc -arch=sm_120 simpleDivergence.cu -o simpleDivergence |
得到结果如下
1 | Data size 16777216 Execution Configure (block 128 grid 131072) |
可以两个内核的运行时间很相近。由于创建容器时没有考虑到获取底层硬件计数器的权限,无法直接通过性能分析工具获得GPU指标。只能从简单的时间进行分析,从时间来看,并没有想象中的分支分化,这是由于CUDA编译器优化导致的结果,它将短的、有条件的代码段的断定指令取代了分支指令(导致分化的实际控制流指令)。
只有在条件语句的指令数小于某个阈值时,编译器才用断定指令替换分支指令。因此,一段很长的代码路径肯定会导致线程束分化。
重写mathkernel,给出函数mathKernel5和mathKernel6
1 | __global__ void mathKernel5(float *c) |
编译并运行
1 | nvcc -arch=sm_120 simpleDivergence.cu -o simpleDivergence |
可以得到如下结果
1 | mathKernel5 (Divergent Loop) elapsed 0.012140 sec |
可见分化对核函数的影响,执行路径串行化,时间被拉长了接近一倍。
重要提示:
- 当一个分化的线程采取不同的代码路径时,会产生线程束分化
- 不同的if-then-else分支会连续执行
- 尝试调整分支粒度以适应线程束大小的倍数,避免线程束分化
- 不同的分化可以执行不同的代码且无须以牺牲性能为代价
3.2.3 资源分配
线程束的本地执行上下文主要由以下资源组成:
·程序计数器
·寄存器
·共享内存
SM处理的每个线程束的执行上下文,在整个线程束的生存期中是保存在芯片内的。因此,从一个执行上下文切换到另一个执行上下文没有损失。每个SM都有32位的寄存器组,它存储在寄存器文件中,并且可以在线程中进行分配,同时固定数量的共享内存用来在线程块中进行分配。
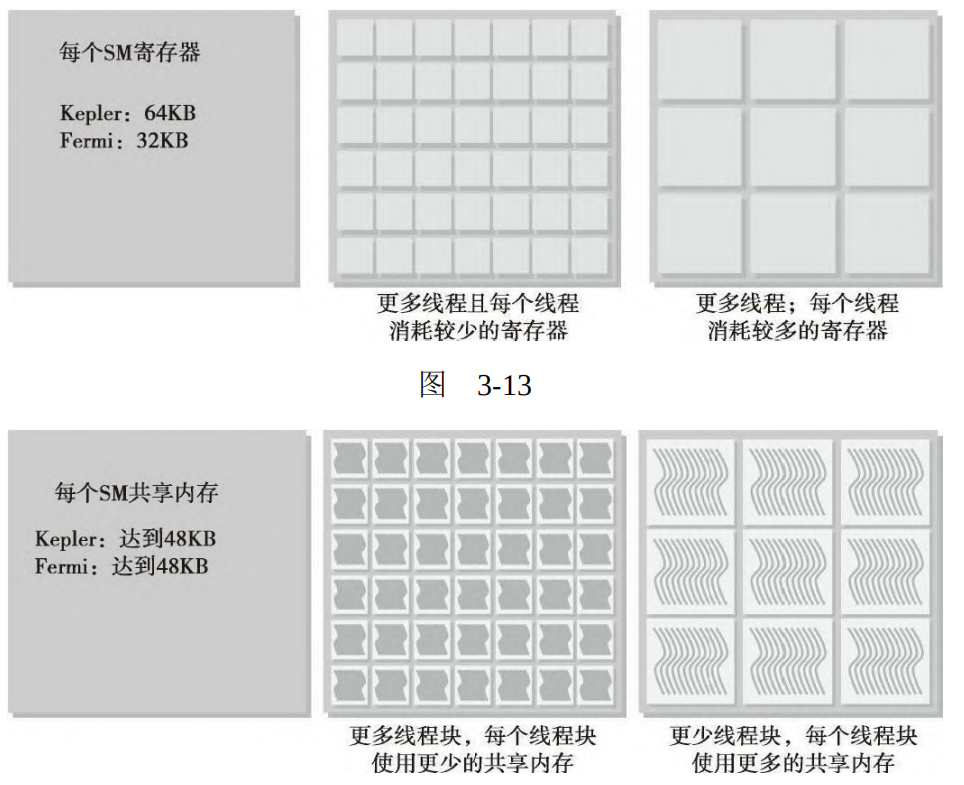
上图显示了:显示了若每个线程消耗的寄存器越多,则可以放在一个SM中的线程束就越少。如果可以减少内核消耗寄存器的数量,那么就可以同时处理更多的线程束。若一个线程块消耗的共享内存越多,则在一个SM中可以被同时处理的线程块就会变少。如果每个线程块使用的共享内存数量变少,那么可以同时处理更多的线程块。
当计算资源(如寄存器和共享内存)已分配给线程块时,线程块被称为活跃的块。它所包含的线程束被称为活跃的线程束。活跃的线程束可以进一步被分为以下3种类型:
·选定的线程束
·阻塞的线程束
·符合条件的线程束
一个SM上的线程束调度器在每个周期都选择活跃的线程束,然后把它们调度到执行单元。
1.活跃执行的线程束被称为选定的线程束。
2.如果一个活跃的线程束准备执行但尚未执行,它是一个符合条件的线程束。
3.如果一个线程束没有做好执行的准备,它是一个阻塞的线程束。
需要满足以下两个条件线程束才能执行:
·32个CUDA核心可用于执行(尽管一个线程束中可能只有8个线程活跃(只有一个块,一个块中有8个线程))
·当前指令中所有的参数都已就绪
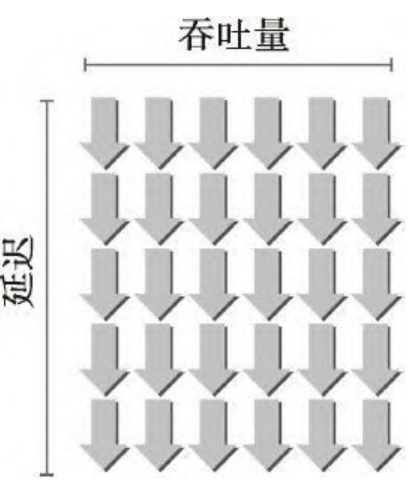
3.2.4 延迟隐藏
SM依赖线程级并行,以最大化功能单元的利用率,因此,利用率与常驻线程束的数量直接相关。在指令发出和完成之间的时钟周期被定义为指令延迟。
考虑到指令延迟,指令可以被分为两种基本类型:
·算术指令
·内存指令
算术指令延迟是一个算术操作从开始到它产生输出之间的时间。
内存指令延迟是指发送出的加载或存储操作和数据到达目的地之间的时间。
对于每种情况,相应的延迟大约为:
算术操作为10~20个周期
全局内存访问为400~800个周期
利特尔法则(Little’s Law)可以为估算隐藏延迟所需要的活跃线程束的数量提供一个合理的近似值:所需线程束数量=延迟×吞吐量
假设在内核里一条指令的平均延迟是5个周期。为了保持在每个周期内执行6个线程束的吞吐量,则至少需要30个未完成的线程束。
吞吐量和带宽
带宽和吞吐量经常被混淆,根据实际情况它们可以被交换使用。吞吐量和带宽都是用来度量性能的速度指标。
带宽通常是指理论峰值,而吞吐量是指已达到的值。
对于算术运算来说,其所需的并行可以表示成隐藏算术延迟所需要的操作数量。对于一个32位的浮点数乘加运算(a+b×c)

对于上图来说
640(吞吐量/容量): 这代表 Fermi 架构中一个 SM(流多处理器)在每个周期内理论上能处理的最大操作数。你可以把它想象成一个工厂车间,每分钟最多能组装 640 个零件。
32(线程束/打包单位): 在 CUDA 架构中,线程不是一个一个执行的,而是以 Warp(线程束) 为单位。一个 Warp 包含 32 个线程。由于所有线程执行同一条指令,因此执行一条指令就相当于一次性完成了 32 个操作。
20(所需并行度): 为了让这个 SM 满负荷工作(即不让硬件闲着),你至少需要同时安排 20 个 Warp 在这个 SM 上运行。
提高并行的方式:
·指令级并行(ILP):一个线程中有很多独立的指令
·线程级并行(TLP):很多并发地符合条件的线程
对内存操作来说,其所需的并行可以表示为在每个周期内隐藏内存延迟所需的字节数。
充足的并行
一个线程束的延迟可以被其他线程束的执行隐藏,用每个SM核心的数量乘以在
该SM上一条算术指令的延迟。
3.2.5 占用率
在每个CUDA核心里指令是顺序执行的。当一个线程束阻塞时,SM切换执行其他符合条件的线程束。
占用率是每个SM中活跃的线程束占最大线程束数量的比值。为了提高占用率,还需要调整线程块配置或重新调整资源的使用情况,以允许更多的线程束同时处于活跃状态和提高计算资源的利用率。

使用这些准则可以使应用程序适用于当前和将来的设备:
·保持每个块中线程数量是线程束大小(32)的倍数
·避免块太小:每个块至少要有128或256个线程(这种规模通常能提供足够的Warp 深度。在一个 SM 中维持较多活跃的线程,能更好地盖过显存访问的漫长等待。)
·根据内核资源的需求调整块大小
·块的数量要远远多于SM的数量,从而在设备中可以显示有足够的并行
·通过实验得到最佳执行配置和资源使用情况
3.2.6 同步
栅栏同步是一个原语,它在许多并行编程语言中都很常见。在CUDA中,同步可以在两个级别执行:
·系统级:等待主机和设备完成所有的工作
·块级:在设备执行过程中等待一个线程块中所有线程到达同一点
cudaDeviceSyn-chronize函数可以用来阻塞主机应用程序,直到所有的CUDA操作(复制、核函数等)完成:
1 | cudaError_t cudaDevicesynchronize(void); |
在一个线程块中线程束以一个未定义的顺序被执行,CUDA提供了一个使用块局部栅栏来同步它们的执行的功能。使用下述函数在内核中标记同步点:
1 | __device__ void _syncthreads(void); |
当__syncthreads被调用时,在同一个线程块中每个线程都必须等待直至该线程块中所有其他线程都已经达到这个同步点。在栅栏之前所有线程产生的所有全局内存和共享内存访问,将会在栅栏后对线程块中所有其他的线程可见。
**不同块中的线程不允许相互同步,因此GPU可以以任意顺序执行块。**这使得CUDA程序在大规模并行GPU上是可扩展的。
3.2.7 可扩展性
对于任何并行应用程序而言,可扩展性是一个理想的特性。例如,若一个CUDA程序在两个SM中是可扩展的,则与在一个SM中运行相比,在两个SM中运行会使运行时间减半。
3.3 并行性的表现
为更好地理解线程束执行的本质,将使用不同的执行配置分析下述的sumMatrixOn-GPU2D核函数。
二维矩阵求和的核函数
1 | __global__ void sumMatrixOnGPU2D(float *A, float *B, float *C, int NX, int NY) |
矩阵大小如下
1 | int nx = 1 << 14; |
编译并执行sumMatrix.cu
1 | nvcc -O3 -arch=sm_120 sumMatrix.cu -o sumMatrix |
3.3.1 ncu检测活跃的线程束
测试一组基础线程块的配置,尤其是大小为(32,32),(32,16),(16,32)和(16,16)的线程块。查看实际占用率,输入命令
1 | ncu --section Occupancy ./sumMatrix 32 32 |
Theoretical Occupancy (理论占用率):在不考虑运行时的延迟和调度的情况下,基于你分配的资源,硬件理论上在一个 SM 中能同时塞下的最大线程束(Warp)比例。
Achieved Occupancy (实际占用率) :在整个运行周期内,SM 中实际活跃的 Warp 数量占最大容量的百分比。
Achieved Active Warps Per SM:在核函数运行期间,平均每个 SM 上有多少个 Warp 是处于“活跃”状态(正在计算、读内存或等待调度)的。
可以得到以下结论:
1.当设置一个块为 1024 线程(32×32)时,SM 剩下的 512 个槽位不足以再塞入另一个完整的块。因此,理论占用率被锁死在 。
2.并发 Warp 越多,GPU 掩盖显存访问延迟的能力就越强。
3.更高的占用率并不一定意味着有更高的性能。
3.3.2 ncu检测内存操作
输入以下命令
1 | ncu --section MemoryWorkloadAnalysis ./sumMatrix 32 32 |
Max Bandwidth :性能金标准。这意味着程序已经利用了显存理论峰值带宽的 83.65%。对于简单的加法核函数,超过 80% 通常意味着访存模式(合并访问)已经接近完美,几乎没有优化空间了。
除上述结果外,命令中还输出了L2 Hit Rate 等结果
| 指标 (Metric) | 16 × 16 (256 threads) | 32 × 32 (1024 threads) | 性能差距 |
|---|---|---|---|
| Memory Throughput | 367.39 Gbyte/s | 280.92 Gbyte/s | +30.8% |
| Max Bandwidth | 88.95% | 83.70% | +5.25% |
| L2 Hit Rate | 25.47% | 2.25% | +23.22% |
| Mem Busy | 22.32% | 19.32% | 16x16 更忙碌 |
可以看出16×16相对32×32来说,吞吐量显著提升,缓存效率的质变。
书中提到了全局加载效率的概念,并得到了以下的结果,以此得到结论:对网格和块启发式算法来说,最内层的维数应该总是线程束大小的倍数。

为测试,我通过以下命令对四组数据进行查询
1 | ncu --metrics l1tex__t_sectors_pipe_lsu_mem_global_op_ld.sum,smsp__sass_inst_executed_op_global_ld.sum ./sumMatrix 16 32 |
四组得到的数据一致:
1 | Section: Command line profiler metrics |
- 一个 Warp 指令处理的数据量 = 。
- 理想状态下的扇区数:GPU 内存访问的最小单位(扇区)是 32 字节。
- 读取 128 字节数据,理想情况下只需要 个扇区。
计算实际“指令-扇区比”:
结论:效率为 100%
可以预见: 即便在 CC 12.0 这种架构上,这种经典的 4 扇区/指令模式依然是衡量 float 类型访存性能的黄金标准。
3.4 避免分支分化
从前文中可以看出,分支分化对程序的影响很大。线程束中的条件执行可能引起线程束分化,这会导致内核性能变差。通过重新组织数据的获取模式,可以减少或避免线程束分化。
3.4.1 并行归约问题
对一个有N个元素的整数数组求和。串行代码如下:
1 | int sum = 0; |
鉴于加法的结合律和交换律,数组元素可以以任何顺序求和。采用以下办法执行并行加法运算:
1.将输入向量划分到更小的数据块中。
2.用一个线程计算一个数据块的部分和。
3.对每个数据块的部分和再求和得出最终结果。
并行加法的一个常用方法是使用迭代成对实现。一个数据块只包含一对元素,并且一个线程对这两个元素求和产生一个局部结果。然后,这些局部结果在最初的输入向量中就地保存。
相邻配对实现:元素与它们直接相邻的元素配对

交错配对实现:根据给定的跨度配对元素。
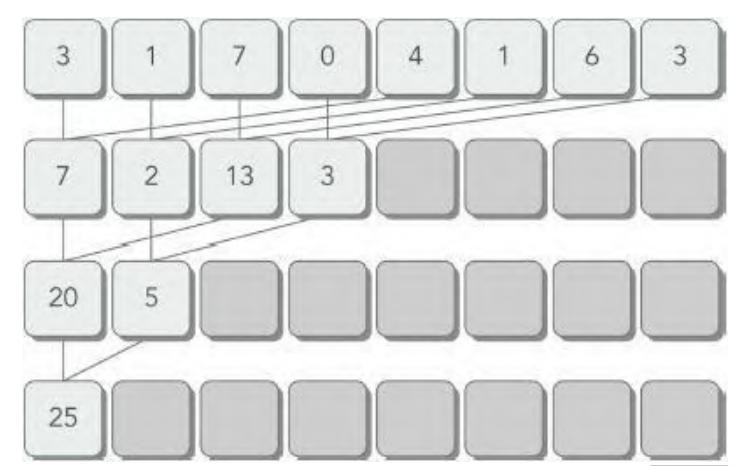
C语言递归实现代码如下:
1 | int recursiveReduce(int *data, int const size) |
在向量中执行满足交换律和结合律的运算,被称为归约问题。
3.4.2 并行归约中的分化
相邻配对方法的内核实现流程:
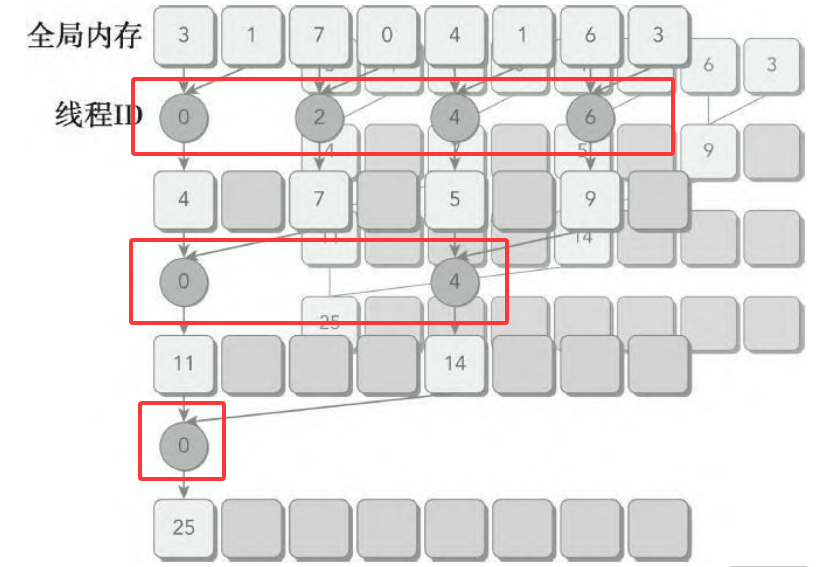
循环中迭代一次执行一个归约步骤。归约是在就地完成的,这意味着在每一步,全局内存里的值都被部分和替代。__syncthreads语句可以保证,线程块中的任一线程在进入下一次迭代之前,在当前迭代里每个线程的所有部分和都被保存在了全局内存中。
核函数代码如下:
1 | __global__ void reduceNeighbored (int *g_idata, int *g_odata, unsigned int n) |
对新入坑cuda的人而言,需要注意线程块之间是完全独立、互不关联的。因此需要对块单独处理,该核函数也是对块级规约,想得到所有数据的总和(全局归约),不能只靠这一个 Kernel 搞定。
在主函数中,设计了线程总数与数组大小一对一的关系,可以保证线程全局索引与需要处理的数组是一对一映射的关系。
1 | dim3 block (blocksize, 1); |
在核函数中通过idata得到对应线程块所有线程的起始索引位置。接着通过规约的形式将线程块的所有线程一一进行规约。最后由0号线程完成对该线程块内所有数字的规约。
编译并运行源码
1 | nvcc -O3 -arch=sm_120 reduceInteger.cu -o reduceInteger |
可以得到如下关键信息
1 | cpu reduce elapsed 0.007615 sec cpu_sum: 2139353471 |
也将作为接下来优化的基准
3.4.3 改善并行归约的分化
可以看到在核函数reduceNeighbored中的代码
1 | if ((tid % (2 * stride)) == 0) |
该语句只对偶数ID的线程为true,所以这会导致很高的线程束分化。在并行归约的第一次迭代中,只有ID为偶数的线程执行这个条件语句的主体,但是所有的线程都必须被调度。且在后续迭代中每次执行的线程数都会减少一半,然而所有线程都会被调度。
假设 stride = 1,我们观察第一个线程束(TID 0 到 31):
- TID 0, 2, 4…30:计算结果为真,执行
if内部。 - TID 1, 3, 5…31:计算结果为假,跳过
if内部。
结果: 在这 32 个线程组成的 Warp 里,有一半线程要走路径 A,一半要走路径 B。硬件必须先让前 16 个跑完,再让后 16 个跑完,效率直接减半。
我们对这部分代码修改:
1 | int index = 2 * stride * tid; |
通过重新组织每个线程的数组索引来强制ID相邻的线程执行求和操作,线程束分化就能被归约了。
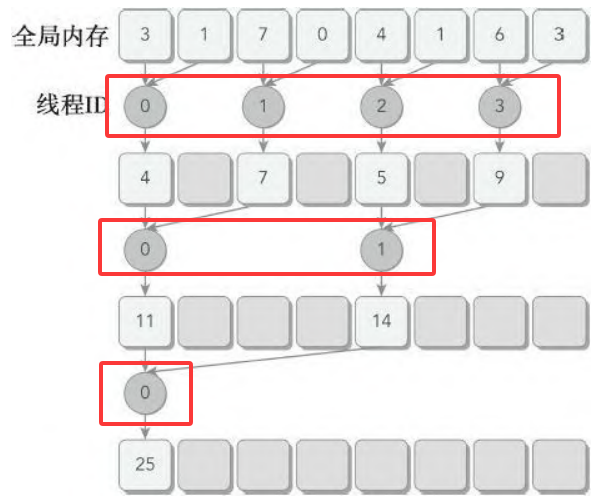
假设 blockDim.x = 128(实际上是512)
一个线程块有128个线程,则有4个wrap
stride = 1时:
- 只有满足
2 * tid < 128的线程,也就是tid < 64。 - Warp 0 (TID 0~31):所有线程的
tid都小于 64。所以 整个 Warp 0 的 32 个线程全部进入if。它们的执行路径 完全相同。 - Warp 1 (TID 32~63):同理,全部小于 64,整个 Warp 1 全部进入
if。执行路径也 完全相同。 - Warp 2 & 3 (TID 64~127):所有线程的
tid都 。这两个 Warp 的所有线程全部跳过if。
以上情况满足了在 GPU 硬件层面:
Warp 内部一致性:只要一个 Warp 里的 32 个线程步调一致,这个 Warp 就运行在最高效率。
调度灵活性:如果一个 Warp(比如 Warp 2)根本不满足 if 条件,调度器会直接跳过它的执行,或者去调度其他任务。它不会像同一个 Warp 内部发生分化那样,被迫在同一个时钟周期内进行“等候”和“掩码操作”。
可以通过结果对比:速度提升了1.5倍左右。
1 | gpu Neighbored elapsed 0.000885 sec gpu_sum: 2139353471 <<<grid 32768 block 512>>> |
通过ncu进行分析可以发现
| 指标 | reduceNeighbored | reduceNeighboredLess | 结论 |
|---|---|---|---|
| 平均指令数 (Ratio) | 143.94 | 116.38 | 下降 19%。执行同样的任务,Warp 跑的指令更少,效率更高。 |
| 显存吞吐量 (%) | 62.85% | 61.06% | 基本没变。说明指令优化的甜头已经尝到了,但内存访问依然是瓶颈。 |
3.4.4 交错配对的归约
与相邻配对方法相比,交错配对方法颠倒了元素的跨度。初始跨度是线程块大小的一半,然后在每次迭代中减少一半。
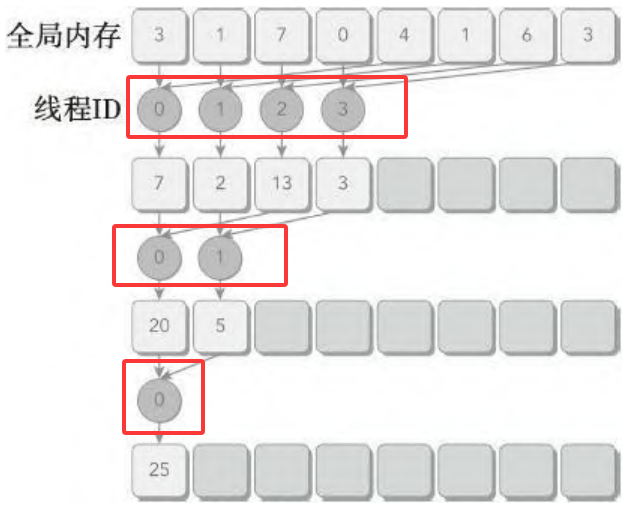
对应的核函数代码如下:
1 | __global__ void reduceInterleaved (int *g_idata, int *g_odata, unsigned int n) |
编译并执行代码
1 | nvcc -O3 -arch=sm_120 reduceInteger.cu -o reduceInteger |
得到关键输出结果如下:
1 | gpu Neighbored elapsed 0.000998 sec gpu_sum: 2139353471 <<<grid 32768 block 512>>> |
可以看到交错配对比相邻配对效果更好。
3.4.4.1 bank冲突
这是因为:
相邻配对在 stride 增大时,活跃线程访问的索引往往会落在同一个 Bank 上。比如当 stride 为 32 的倍数时,多个线程会同时撞向同一个 Bank 的不同地址,产生严重的 Bank Conflict。
交错配对: 由于 stride 的初始值很大(blockDim.x / 2)并且是逐渐减小的,线程 tid 访问的是 idata[tid]。在绝大多数步长下,活跃线程访问的地址是连续的,天然地避开了同一个 Bank,从而完全消除了 Bank 冲突。
例如:
相邻配对情况下
情况 A:当 stride = 1 时
- 线程 0 访问
index 0Bank 0 - 线程 1 访问
index 2Bank 2 - 线程 16 访问
index 32Bank 0 - 结果:产生 2 路 Bank 冲突(每个 Bank 有两个线程在排队)。
情况 B:当 stride = 16 时
- 线程 0 访问
index 0() Bank 0 - 线程 1 访问
index 32() Bank 0 - 线程 2 访问
index 64() Bank 0 - 结果:Warp 内所有活跃线程都试图访问 Bank 0 的不同位置。硬件被迫把原本并行的操作变成了串行,性能缩水 32 倍。
交错配对情况下
- 不管
stride是多少:- 线程 0 永远访问
index 0Bank 0 - 线程 1 永远访问
index 1Bank 1 - 线程 2 永远访问
index 2Bank 2 - …
- 线程 31 永远访问
index 31Bank 31
- 线程 0 永远访问
在一个 Warp 内部,32 个线程访问的 Bank ID 分别是 0 到 31。没有任何两个线程在抢同一个 Bank。硬件可以一个时钟周期内完成所有读写。
3.4.4.2 合并内存访问
相邻配对:线程 0 和 1 访问 idata[0] 和 idata[2]。这在内存中是不连续的(跳过了索引 1)。随着步长增加,这种“空洞”越来越大。
交错配对:
1 | idata[tid] += idata[tid + stride]; |
线程 0 到 31 访问的是 idata[0...31]。这是一组完全连续的 128 字节地址。
总结:由于bank冲突和合并内存访问的相关原因,可以得到交错配对比相邻配对更好的结论。
3.5 展开循环
循环展开是一个尝试通过减少分支出现的频率和循环维护指令来优化循环的技术。循环体的复制数量被称为循环展开因子,迭代次数就变为了原始循环迭代次数除以循环展开因子。
考虑以下代码
1 | for(int i = 0; i < 100; i++) |
如果重复操作循环体,可以发现迭代次数减少到了原始循环的一半:
1 | for(int i = 0; i < 50; i += 2) |
从高级语言层面上来看,循环展开使性能提高的原因可能不是显而易见的。这种提升来自于编译器执行循环展开时低级指令的改进和优化。
3.5.1 展开的归约
对下面的核函数reduceUnrolling2来说
1 | __global__ void reduceUnrolling2 (int *g_idata, int *g_odata, unsigned int n) |
在执行循环之前,先让每个线程把自己负责的第一个数据和跨度为 blockDim.x 的第二个数据相加。
全局数组索引被相应地调整,因为只需要一半的线程块来处理相同的数据集。请注意,这也意味着对于相同大小的数据集,向设备显示的线程束和线程块级别的并行性更低。因为现在每个线程块处理两个数据块,我们需要调整内核的执行配置,将网格大小减小至一半。
1 | reduceUnrolling2<<<grid.x / 2, block>>>(d_idata, d_odata, size); |
运行程序得到以下结果
1 | gpu Neighbored elapsed 0.000830 sec gpu_sum: 2139353471 <<<grid 32768 block 512>>> |
可以发现在一个线程中有更多的独立内存加载/存储操作会产生更好的性能,因为内存延迟可以更好地被隐藏起来。
同时编写了reduceUnrolling4和reduceUnrolling8核函数(展开因子分别为4和8)
得到以下结果
1 | cpu reduce elapsed 0.006318 sec cpu_sum: 2139353471 |
执行以下命令:
1 | ncu --metrics dram__throughput.avg.pct_of_peak_sustained_elapsed ./reduceInteger |
可以总结得到如下表格:
| 算法阶段 | 核心优化点 | 执行时间 (ms) | 带宽利用率 (%) | 评价 |
|---|---|---|---|---|
| Neighbored | 基础归约 (取模运算) | 0.893 | 62.90% | 最差:严重的线程束分化。 |
| Neighbored2 | 消除分化 (连续映射) | 0.525 | 61.02% | 大幅提升:指令流变顺畅。 |
| Interleaved | 交错配对 (连续访存) | 0.502 | 52.24% | 平稳:解决了 Bank 冲突,但总线压力仍不足。 |
| Unrolling2 | 2路展开 (块减半) | 0.361 | 89.98% | 质变:开始真正压榨显存带宽。 |
| Unrolling4 | 4路展开 | 0.311 | 96.11% | 巅峰:几乎达到了硬件物理带宽极限。 |
| Unrolling8 | 8路展开 | 0.475 | 95.84% | 性能倒退:块太少,无法掩盖延迟。 |
| UnrollWarp8 | 展开 + Warp优化 | 0.309 | N/A | 极致:进一步消除循环开销。 |
3.5.2 展开线程的归约
线程束展开
__syncthreads是用于块内同步的。在归约核函数中,它用来确保在线程进入下一轮之前,每一轮中所有线程已经将局部结果写入全局内存中了。
当只剩下32个或更少线程(即一个线程束)的情况时。因为线程束的执行是SIMT(单指令多线程)的,每条指令之后有隐式的线程束内同步过程。
因此可以把最后6个迭代展开,主要作用如下:
消除开销:每一轮原本需要的循环判定(stride > 0)和同步指令(__syncthreads)全都被删掉了。
基于reduceUnrolling8,线程束的展开可以添加到归约核函数中
1 | if (tid < 32) |
volatile 关键字:**** 它的作用是告诉编译器:“这些数据随时可能被其他线程修改,请不要把它们缓存在寄存器里,每次都必须实打实地读写内存。
在 NVIDIA GPU 硬件中,Warp 是基本的执行单元。
- 同步执行:一个 Warp 里的 32 个线程是“捆绑”在一起的。在物理层面上,它们在同一个时钟周期内执行相同的指令。
- 隐式同步(Implicit Synchronization):既然大家都在同一时间做同样的事情,那么当线程 0 需要读取线程 16 计算出的结果时,线程 16 必然已经完成了它的加法指令。
观察输出:
1 | gpu Unrolling8 elapsed 0.000311 sec gpu_sum: 2139353471 <<<grid 4096 block 512>>> |
可以看到了得到了不少的提升
3.5.3 完全展开的归约
如果编译时已知一个循环中的迭代次数,就可以把循环完全展开。每个块的最大线程数都是1024,且这些归约核函数中循环迭代次数是基于一个线程块维度的,所以完全展开归约循环是可能的:
1 | __global__ void reduceCompleteUnrollWarps8 (int *g_idata, int *g_odata, |
3.6 动态并行
CUDA的动态并行允许在GPU端直接创建和同步新的GPU内核。在一个核函数中在任意点动态增加GPU应用程序的并行性。动态并行提供了一个更有层次结构的方法,在这个方法中,并发性可以在一个GPU内核的多个级别中表现出来。
3.6.1 嵌套执行
内核执行分为两种类型:父母和孩子。父线程、父线程块或父网格启动一个新的网格,即子网格。子线程、子线程块或子网格被父母启动。子网格必须在父线程、父线程块或父网格完成之前完成。只有在所有的子网格都完成之后,父母才会完成。
父网格和子网格共享相同的全局和常量内存存储,但它们有不同的局部内存和共享内存。
3.6.2 在GPU上嵌套Hello World
我们通过创建一个核函数,使其用动态并行来输出“Hello World”进行理解。
1 | __global__ void nestedHelloWorld(int const iSize, int iDepth) |
该父网格在一个线程块中有8个线程。然后,该父网格中的线程0调用一个子网格,该子网格中有一半线程,即4个线程。之后,第一个子网格中的线程0再调用一个新的子网格,这个新的子网格中也只有一半线程,即2个线程,以此类推,直到最后的嵌套中只剩下一个线程。
编译并执行程序
1 | nvcc -arch=sm_120 -rdc=true nestedHelloWorld.cu -o nestedHelloWorld -lcudadevrt |
可以得到以下结果
1 | (cuda_env) root@63320d55395d:~/cuda_learn/cuda_program/CodeSamples/chapter03# ./nestedHelloWorld |
动态并行的最大嵌套深度限制为24,但是实际上,在每一个新的级别中大多数内核受限于设备运行时系统需要的内存数量。因为为了对每个嵌套层中的父网格和子网格之间进行同步管理,设备运行时要保留额外的内存。
3.6.3 嵌套归约
归约可以被表示为一个递归函数。在CUDA里使用动态并行,可以确保CUDA里的递归归约核函数的实现像在C语言中一样简单。
采用下图的规约办法
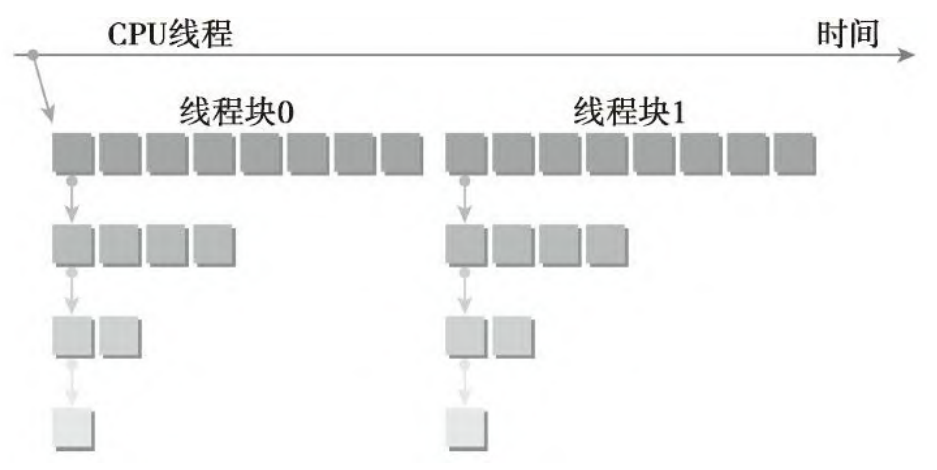
核函数代码如下
1 | __global__ void gpuRecursiveReduce (int *g_idata, int *g_odata, |
编译并运行nestedReduce.cu
1 | nvcc -arch=sm_120 -rdc=true nestedReduce.cu -o nestedReduce -lcudadevrt |
本文不过多介绍嵌套规约内容,仅知道有这种方式存在即可。有需求的同学自行翻阅书本内容或查阅相关资料。
3.7 总结
本章从硬件的角度分析了内核执行。在GPU设备上,CUDA执行模型有两个最显著的特性:
- 使用SIMT方式在线程束中执行线程
- 在线程块与线程中分配了硬件资源
这些执行模型的特征使得我们在提高并行性和性能时,能控制应用程序是如何让指令和内存带宽饱和的。不同计算能力的GPU设备有不同的硬件限制,因此,网格和线程块的启发式算法在为不同平台优化内核性能方面发挥了非常重要的作用。